Unifews: You Need Fewer Operations for Efficient Graph Neural Networks
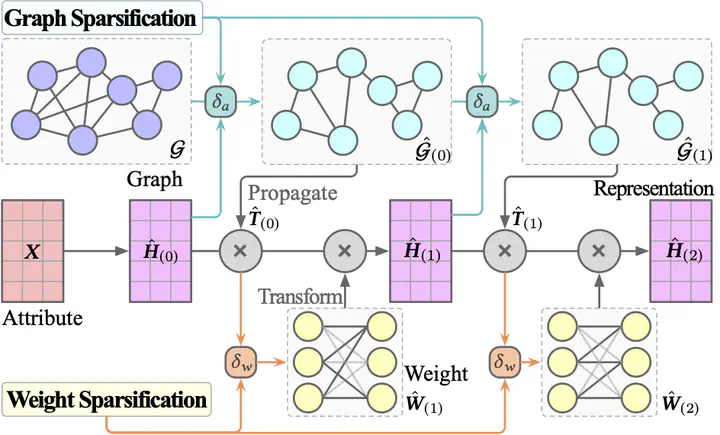
Progressive entry-wise sparsification for both graph and weights.
Theoretical spectral bounds for GNN propagation and transformation sparsification.
Graph Neural Networks (GNNs) have shown promising performance, but at the cost of resource-intensive operations on graph-scale matrices. To reduce computational overhead, previous studies attempt to sparsify the graph or network parameters, but with limited flexibility and precision boundaries. In this work, we propose Unifews, a joint sparsification technique to unify graph and weight matrix operations and enhance GNN learning efficiency. The Unifews design enables adaptive compression across GNN layers with progressively increased sparsity, and is applicable to a variety of architectures with on-the-fly simplification. Theoretically, we establish a novel framework to characterize sparsified GNN learning in view of the graph optimization process, showing that Unifews effectively approximates the learning objective with bounded error and reduced computational overhead. Extensive experiments demonstrate that Unifews achieves efficiency improvements with comparable or better accuracy, including 10-20× matrix operation reduction and up to 100× acceleration on graphs up to billion-edge scale.